ATV: a very special delivery - Lesson notes
(Jules Verne, "From the Earth to the Moon", 1865)

1 - Controlling a collision

Essentially, a docking manoeuvre is a controlled, inelastic collision. You allow two objects to collide and stick together at a relatively low velocity. So, even though both objects are moving at about 8 km s-1, they approach each other at a few centimetres per second. There are a number of reasons for this.
Since there is relatively low friction compared to on Earth at ground level, any stabilising actions of the thrusters must be performed wisely, otherwise it could throw the ATV wildly off-course. If small adjustments are the only adjustments that can be made, you really want to be approaching the docking point at a very small relative velocity. Think about a driver reversing a car into a very tight space, with a one centimetre clearance on either side. He wouldn’t want do this quickly would he? It is the same principle. However, for the ATV, this process is fully automated using information from its own rendezvous sensors, whilst being monitored from the ATV Control Centre in Toulouse, France.
Furthermore, if you have ever witnessed the inelastic collision of two masses on an air track in a laboratory, you will appreciate that momentum is conserved before and after the collision (Principle of conservation of momentum.) The last thing scientists want is for a 20 tonne mass to bump heavily into the ISS. Apart from the damage, it would affect the velocity, and therefore the trajectory of the ISS.
If the ISS has a mass of approximately 250 tonnes and the ATV is approximately 20 tonnes, we can show that the increase in velocity of the docked ATV and ISS should be about a tenth of that of the relative approach velocity. We will simplify matters and treat this as a linear collision. For the principle of conservation of momentum:

This can be simplified, in the ISS observer’s frame, and rearranged to give:

This represents an increase in orbital speed, Δv, for the ISS after docking, relative to the approach speed of the ATV. If we consider (a few centimetres per second), the increase in orbital speed of the ISS is
(a few centimetres per second), the increase in orbital speed of the ISS is  which, compared with the ISS orbital speed of 8 km s-1, is fortunately tiny!
which, compared with the ISS orbital speed of 8 km s-1, is fortunately tiny!
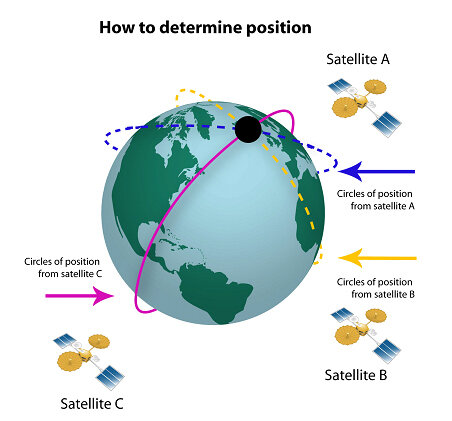
2 - The ATV: “Where am I?”

In the early stages of navigation, the ATV uses a combination of star tracker and Global Positioning System (GPS) data to get closer to the ISS. In a similar way that humans have used the stars to navigate on Earth for many centuries, star tracker – a modern day equivalent to the sextant – is able to recognise different constellations in the sky to calculate its own orientation in space. In addition, GPS, measures angles between the orbiting GPS satellites in order to give positional information. This is the same GPS technology that we use here on Earth.
The GPS receiver uses the network of at least 24 operational GPS satellites. Each satellite orbits with a period of twelve hours such that at any point in time on Earth, a GPS receiver can receive an electromagnetic time-code signal from at least four of the satellites as well as positional data of the individual satellites. The same is true for the ATV in space. The time-codes transmitted by the satellites are all synchronised according to atomic clocks. The GPS receiver also requires a synchronised clock onboard so that it can calculate the differences in time codes (which are travelling at the speed of light) and hence the distance to each satellite. The GPS receiver will calculate the distance to each of the satellites and find the singular point where the surfaces of the spheres, of radii corresponding to the distances from each of the satellites, intersect in space, in order to calculate its position. This is known as three-dimensional trilateration.
If we know, for example,that the time-code signal from satellite A corresponds to tA=0.0796963586 s and from satellite B tB=0.0832568645 s, we can work out the distance to each satellite:
Distance to satellite A, dA=tAc=23908.90758 km
Distance to satellite B, dB=tBc=24977.05935 km

Atomic clocks are extremely expensive and would make the cost of owning a GPS receiver prohibitive, which is why, on Earth, each GPS receiver has an internal quartz clock instead. Unfortunately, this is not as accurate as an atomic clock. If a GPS receiver on Earth is slightly out of synch, it will give a tiny mistake of a few thousandths of seconds for each satellite. Referring to the previous satellites A and B, the times could be, for example tA=0.0797963586 s and tB=0.0835568645 s. This would correspond to:
Satellite A:
dA=tAc=23938.90758 km and a resulting circle error of 30 km
Satellite B:
dB=tBc=25067.05935 km an a resulting circle error of 90 km
This intersection point in the map would give a completely wrong position! Fortunately a third satellite signal is received and the receiver can make an adjustment based on each of the time-code signals it receives. Indeed, each of the distances will be proportionally incorrect and won’t intersect at a single point. So, the receiver adjusts its internal clock such that the measured distances intersect at a unique point. The receiver is constantly doing this, so you could argue that you have access to a very accurate clock if you have your own car satellite navigation system. For three-dimensional positioning, a fourth satellite is required. This will allow us to find the right position of a plane, in order to provide altitude information.
Soon, Galileo will be Europe’s own global navigation satellite system, providing a highly accurate, guaranteed, global positioning service under civilian control (see related link on right column).
This exercise is partially based on the `Lift-Off’ exercises published by ESA BR-223.
3 - Rendezvous in space
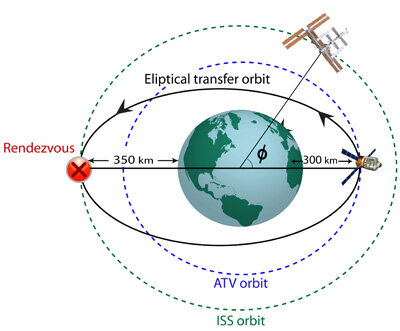
The best moment to launch (“launch window”) the ATV is when Kourou is almost underneath the position of the ISS orbit. This is known as the launch window and means that, when launched, the ATV will be put into an orbit which is in the same plane of the ISS, resulting in fewer correction manoeuvres during the transfer orbit.
From Kepler’s Third Law, we can work out the orbital period of the elliptical transfer orbit. Firstly, we have to find out the value of the constant k in Kepler’s Third Law. For this purpose, we consider a circular orbit to be a special case of an elliptical orbit.

(this exercise is based on the `Lift Off’ exercised published by ESA BR-223)
4 - How far to docking, Sir?

A retro-reflector will reflect light back in the same direction as the source, so the distance measured will be a direct line-of-sight distance. For example, if the pulses are returning with a 1.5µs delay, then we can calculate the distance as follows:

Remembering, of course, that the time has to be divided by two (the time measured is the time for the pulse to travel to and from the retro-reflector). The telegoniometer provides 10000 pulses per second at a different wavelength, ensuring that the final approach is carefully monitored in conjunction with the videometer sensors.
5 - Re-boosting – why such a low orbit?

3.8 x 10-12 kg m-3.
(The actual density varies according to solar activity and whether it is day or night. This approximate value over a year for mean levels of solar activity is taken from the MSISe-90 Atmosphere Model).
We can calculate the drag force FD at a velocity v using  where CD is the (dimensionless) drag coefficient of the object, ρ is the density of the fluid (the residual atmosphere) and A is the cross-sectional area of the moving object.
where CD is the (dimensionless) drag coefficient of the object, ρ is the density of the fluid (the residual atmosphere) and A is the cross-sectional area of the moving object.
The drag coefficient of the ISS is about 2,07 and for ATV 2,4. The cross sectional area of the ISS can vary between about 700 m2 and 2300 m2, depending on the ISS configuration. If we consider A=1000 m2, this results in a typical drag force of 0,25 N. The decrease in velocity corresponding to this force is

If we consider a typical day, then t=86400 s and Δv=0.09 m s-1, giving a decrease of orbital height of about 100 m per day (see Section 6).
Despite the low atmospheric density at 400 km, there are still several million billions of atoms per cubic centimetre and this results in drag on the ISS, causing it to lose height over time. You would think that the issue of having to re-boost ISS regularly would be a good argument for putting it into a higher orbit. This way, there would be no need to transport large amounts of fuel on-board the ATV to carry out the re-boosting operations.
If only it were that simple! Let’s see how much energy is required to get to such an orbital height.
To find out how much energy is required (the work done, Wg) to move a mass from the surface of the Earth (RE) to an altitude of 400 km (RE + 400 km), we need to calculate the difference in gravitational potential energy (GPE) at these two points. Work done = GPE at 400 km – GPE at Earth’s surface:

So, each kilogramme of mass requires 3.7 × 106 J of energy to move to 400km this distance from Earth. This is the work done against gravity alone. When you start to include the mass of the ATV body, its fuel and drag due to the atmosphere during lunch, you can see quite rapidly that this requires huge amounts of energy. In fact, the work done against gravity alone is of the order of 7.0 × 1010 J (this is comparable to the energy consumed by an average automobile in one year). Hence the need for a powerful launch vehicle such as the Ariane 5 rocket. (See link on the right column)
Obviously, the higher the orbit, the more the energy required to reach it. This is the principle reason that ISS is in a Low Earth Orbit (LEO) at 400km. Any higher and more fuel would be needed to get there, resulting in much higher launch costs.
6. Maintaining orbital velocity

We can do this by equating the gravitational force between two masses (namely the Earth and ISS) with the centripetal force required to keep ISS in orbit. In other words, gravity provides the centripetal force.
The gravitational force between two masses M and m, separated by a distance r is given by

Centripetal force is given by F=ma. If we assume circular motion and substitute 
for the centripetal acceleration, then we have 
So, we have

Rearranging to find v:

Giving just under 8 km s-1. At this velocity, you could fly from Paris to Berlin (877km) in less than two minutes! The ATV is fitted with 4 re-boosting thrusters, each of which can generate 490 N of thrust. When the ATV is docked with ISS, two of these thrusters re-boost the orbit and produce the required Δv. Depending on the height of ISS, a typical re-boost burn may last about half an hour to increase the orbital height by about 30-50 km.
7. Air resistance upon re-entry

Once the ATV’s re-supply mission is complete (approximately 6 months), it will leave ISS and be bound for re-entry into the Earth’s atmosphere. Unlike the manned shallow-angle Space Shuttle re-entries, the ATV will move into a steep and destructive trajectory, causing it to start the re-entry at a velocity approaching 8 km s-1. As it descends, the atmospheric density will increase, causing drag.
Whereas the Ariane 5 rocket has an aerodynamic design, to minimise the effects of atmospheric drag during its launch, this is not the case for the ATV. Coupled with the fact that it will be travelling much faster, it will experience very high levels of heating. If it enters the Earth’s atmosphere at just under 8 km s-1 the resulting compression of the air in front of the ATV will create a gas shock layer that will reach a temperature high enough to dissociate and ionise atoms in the air, creating a plasma. Clearly, this is a destructive entry. Between 70 and 50 km the ATV will start to dismantle and will repeatedly break up into smaller and smaller fragments, due to the high temperatures experienced. The resulting fragments and waste will completely burn up in the atmosphere, but there is always a small risk that a fragment of debris will fall to ground level, which is why such destructive re-entries are made over the Pacific Ocean.