Spatial Keplerian Map
Background
Studying the ebb and flow of regions within a dynamical environment is important for understanding particle transport. These problems are analogous to the study of waste transport in the ocean. Just as ocean current systems carry waste between the Northern and Southern Hemispheres, dynamical structures in Hamiltonian systems similarly govern the motion of spacecraft and other propellant-less objects. Therefore, identifying these dynamical structures is crucial for trajectory design and space debris disposal.
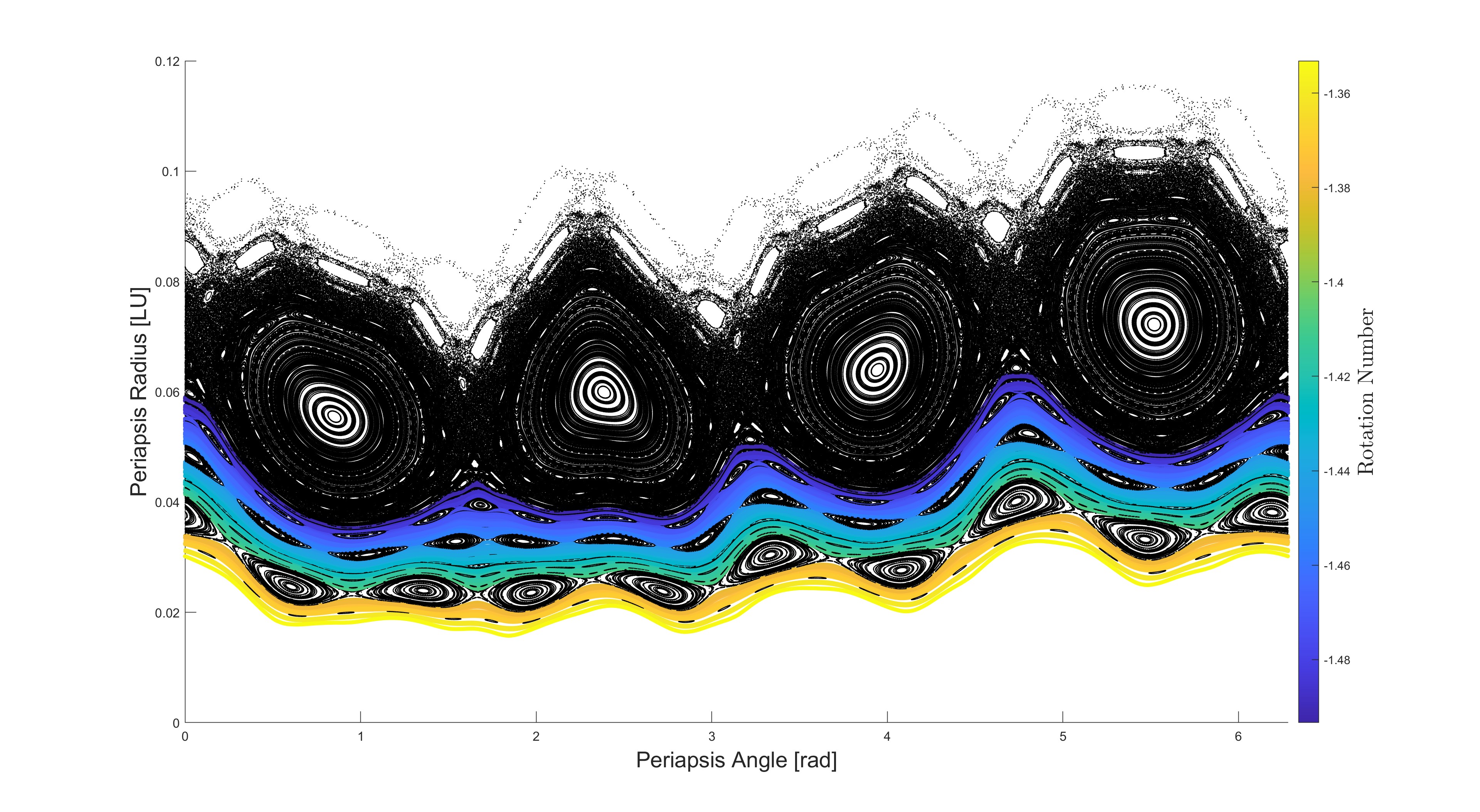
A commonly studied Hamiltonian system is the planar restricted three-body problem (PR3BP). For visualization, periapsis maps in the PR3BP generate a 2-dimensional surface that records trajectory states at a periapsis event. Functioning as a cross-sectional slice of space, these maps reveal many underlying dynamical structures. However, this insight often comes at a significant computational cost. To avoid this cost, an analytical approximation of the periapsis map was developed for the PR3BP: the Keplerian map [1]. It analytically approximates consecutive periapsis states. Additionally, the Keplerian map is a symplectic map, enabling the use of tools from symplectic geometry [2,3].
The Keplerian map has been used to identify dynamical objects such as rotational invariant curves (RICs), cantori, and resonant island chains, which correspond to various invariant tori in the full phase space [4]. Interestingly, these invariant tori act as barriers that shield orbital shells around the primary body, thereby restricting the transport of particles and space debris.
Project Overview
A major drawback of the Keplerian map is its planar assumption in the R3BP. In this project, we aim to extend the Keplerian map to the spatial problem. Specifically, we will develop a discrete update for the additional Delaunay action and angle between subsequent periapsis passages using the Lagrange Planetary Equations under a 3rd body perturbation. With the extension to a higherdimensional phase space, the Keplerian map becomes 4-dimensional, making visualization less straightforward.
The validity of the spatial Keplerian map will be explored in the Earth-Moon R3BP, modeling the cislunar environment. In particular, numerical integration will be used to determine where the analytical spatial map provides a reasonable approximation of the true system dynamics.
After validating the spatial map, the numerical tools used to identify structures (such as invariant tori) from the map in the planar case will be extended to the spatial problem [5]. RICs will be replaced with their higher-dimensional analogs, rotational invariant surfaces (RISs). RISs correspond to families of Lagrangian 3-tori in phase space. These families of 3-tori shield orbital shells centered on the primary from particle transport. The development of the spatial Keplerian map and the identification of rotational invariant surfaces have important applications for planetary defense in the Earth-Moon R3BP. These dynamical structures may significantly limit the transport of jettisoned debris over several centuries in the full ephemeris.
References
[1] S. D. Ross and D. J. Scheeres, “Multiple Gravity Assists, Capture, and Escape in the Restricted Three- Body Problem,” SIAM Journal on Applied Dynamical Systems, Vol. 6, No. 3, 2007, pp. 576–596, https://doi.org/10.1137/060663374
[2] R. Mackay, “Flux over a saddle,” Physics Letters A, Vol. 145, No. 8, 1990, pp. 425–427, https://doi.org/10.1016/0375-9601(90)90306-9.
[3] J. D. Meiss, “Symplectic maps, variational principles, and transport,” Rev. Mod. Phys., Vol. 64, Jul 1992, pp. 795–848, https://doi.org/10.1103/RevModPhys.64.795.
[4] M. Morimitsu, M. Bando, and S. Hokamoto, “Detecting Unstable Resonant Orbits via Keplerian Map,” 2025 AAS/AIAA Space Flight Mechanics Meeting, Vol. AAS 25-353, 08 2025.
[5] E. Sander and J. Meiss, “Birkhoff averages and rotational invariant circles for area-preserving maps,” Physica D: Nonlinear Phenomena, Vol. 411, Oct. 2020, p. 132569, https://doi.org/10.1016/j.physd.2020.132569.