Reinforcement Learning for the Keplerian TSP

Background

The Keplerian Travelling Salesperson Problem (KTSP) is a combinatorial problem associated with multi-target mission design. A spacecraft needs to visit a number of destinations (targets) in a single mission, and the efficiency (propellant consumption) of this mission depends greatly on the order and timings of each visit (the sequence). Hence, a sequence must be selected to achieve minimal propellant consumption.

Despite the simple formulation, this is a combinatorial problem that is extremely time-consuming to solve, to the point that globally optimal (exact) solutions for large-scale problems (reasonably many targets and fine resolution of time discretisation) are impossible to produce in a reasonable space of time. Recent work at ACT has produced benchmark mission scenarios, and an integer linear programming (ILP) approach to generate exact solutions for these scenarios. However, due to the time issue outlined above, the larger instances have proven too combinatorially complex to solve in a reasonable time.

Project goal

The aim of this project is to assess the extent to which artificial neural networks (ANNs) can be used to shorten the time in which the ILP solver finds an exact solution. The ANN (whose computational time is very small) would be trained to output a sequence of visits given a list of targets. This solution, whilst not necessarily exact, would enable establishing an upper bound for the ILP solver, meaning that branches exceeding it could be pruned. Depending on the quality of this bound (how close it is to the exact solution), the ILP solver would converge faster, evading the need to establish this bound through its own exploration. Existing methods such as the 2-opt algorithm can be used to quickly generate such bounds, but for problems with large numbers of targets, they are not good enough to sufficiently lower the computational time of the ILP solver. Hence, ultimately, the goal of the project is to exceed the performance of fast heuristics such as 2-opt for larger problems which present a challenge to the ILP approach.

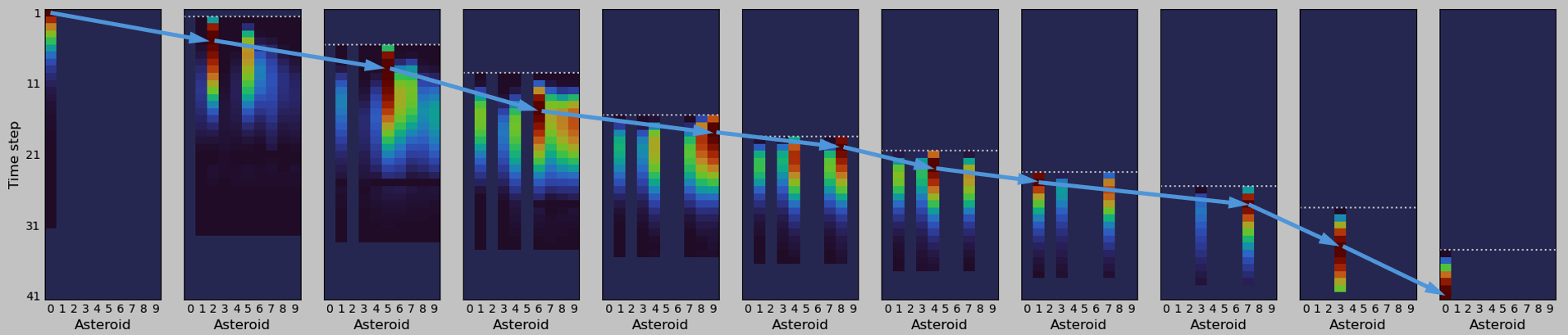
Machine learning approach

Machine learning solutions to the KTSP are made possible by ANN architectures based on the pointer network [1]. This casts the problem as if it were a machine translation problem, where the input ‘sentence’ is a list of nodes and the output ‘sentence’ is an ordered set of these. At each solution step, the pointer network assigns a probability distribution to each node. Near the start of training (performed using reinforcement learning), most of these probabilities have similar values, meaning that the ANN is not biased in favour of any particular node, but throughout training it learns which nodes constitute better choices, and once trained, the choice of nodes leading to the best solutions receive the highest probabilities. The figure illustrates this with heatmaps representing probabilities (computed by the trained pointer network) of selecting a given target/time combination for 10 successive visits in a sequence. A different colour is used to represent masked-out options (visited targets, past times and future times kept free to avoid exceeding the time limit).

The ANN would be trained on randomly-generated clusters of targets and would then produce solutions for any unseen cluster within the range of orbits used for training. Whilst existing research has addressed small clusters [2], these can often be solved well with the ILP approach so the key aim of the research is to enable ANNs to solve much larger problems, that present a challenge to the ILP solver.

References

[1] O. Vinyals, M. Fortunato, N. Jaitly, Pointer networks, Advances in Neural Information Processing Systems 28 (2015), doi:10.48550/arXiv.1506.03134.

[2] Z. Chen, Y. Bai, Y. Zhao, X. Chen, Rapid sequence generation for active debris removal mission based on attention mechanism and pointer network, IEEE Access 12 (2024) 95020–95034, doi:10.1109/ACCESS.2024.3425161.