Reinforcement Learning for Solar Sailing to the Outer Solar System

Project overview

Solar-propelled spacecraft have been theorized since the beginning of rocketry and space exploration. They have drawn considerable interest due to the potential for very long, fuel-free missions. The Japan Aerospace Exploration Agency (JAXA) successfully demonstrated solar sailing in 2010 with the IKAROS mission. In recent years, the National Aeronautics and Space Administration (NASA) has been scaling and developing the technology to sails in the thousand-square-meter range, aiming to prove their effectiveness for non-Keplerian orbits and deep-space missions.

Solar sail missions come with major challenges in system design, attitude control, and trajectory optimization. Missions to the outer solar system may require complex trajectory design due to the limited thrust, reduced control authority far from the Sun, and stringent temperature constraints close to the Sun.

Multiple approaches have been tested for solar sail trajectory design, such as evolutionary neurocontrol [1], indirect methods from optimal control theory [2], and Lyapunov-inspired Q-law methodologies [3].

In this project, modern reinforcement learning and machine learning approaches have been developed with the objective of performing a time-optimal transfer from Earth’s orbit (1 AU) to Neptune’s distance (20 AU), while satisfying solar-proximity or temperature constraints.

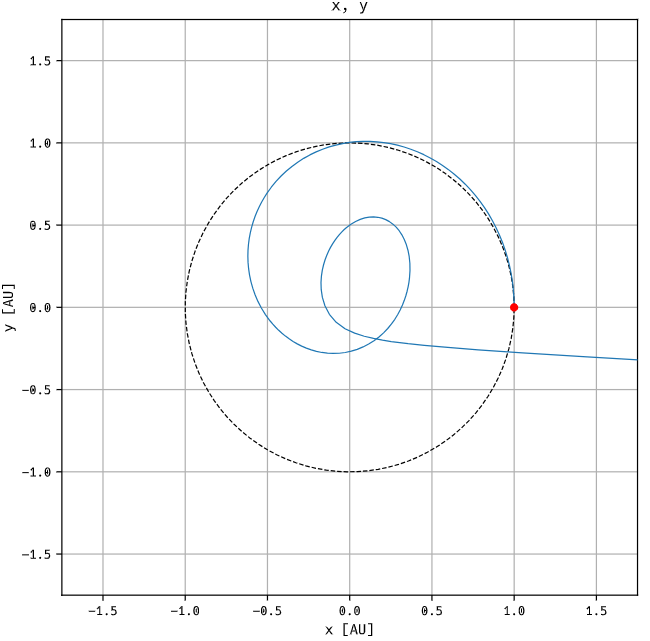
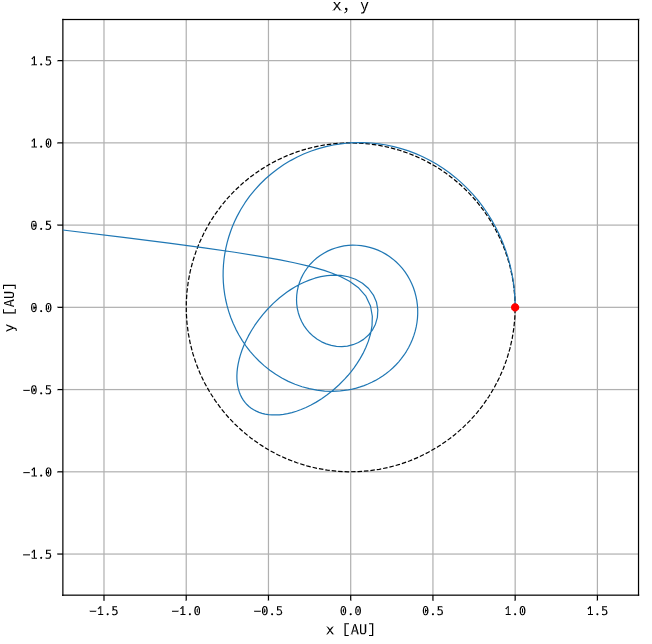
The optimization is based on two main steps. First, a policy network is trained with Proximal Policy Optimization (PPO) [4] until the spacecraft reaches the target distance. Subsequently, the orbit is further optimized using a Neural Ordinary Differential Equation (Neural ODE) correction, reducing transfer times.

As shown in the figures, the topology of the resulting orbital trajectories can be quite complex. In particular, the solar sail first spirals into a lower-energy orbit and then successfully raises its apoapsis by performing multiple photonic solar assists.

Compared to the evolutionary neurocontrol results in Dachwald [1], this approach leads to a reduction in flight time of 10–20%, depending on the sail strength.

References

[1] Dachwald, Bernd. (2005). Optimal Solar Sail Trajectories for Missions to the Outer Solar System. Journal of Guidance, Control, and Dynamics. 28. 1187-1193. 10.2514/1.13301.

[2] Kenshiro Oguri, Gregory Lantoine, Indirect trajectory optimization via solar sailing primer vector theory: Minimum solar-angle transfers, Acta Astronautica, Volume 211,

[3] Lorenzo Niccolai, Alessandro A. Quarta, Giovanni Mengali. Solar sail heliocentric transfers with a Q-law, Acta Astronautica

[4] Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O., “Proximal Policy Optimization Algorithms”, arXiv e-prints, Art. no. arXiv:1707.06347, 2017. doi:10.48550/arXiv.1707.06347.

[5] Chen, R. T. Q., Rubanova, Y., Bettencourt, J., and Duvenaud, D., “Neural Ordinary Differential Equations”, arXiv e-prints, Art. no. arXiv:1806.07366, 2018. doi:10.48550/arXiv.1806.07366.