Accelerated Taylor models for verified integration
Background
Modern spacecraft guidance, navigation, and control (GNC) systems face an inherent tension between autonomy and assurance. Current verification practices offer little comfort: even state-of-the-art spacecraft designs rely heavily on Monte Carlo simulations, which explore behavior through random sampling rather than mathematical certainty. Despite massive computational investments, these simulations can only provide probabilistic confidence in system performance — never formal guarantees. As a result, mission designers must trade off between computational cost and confidence level, leaving both AI-based and conventional systems vulnerable to unverified edge cases. The absence of scalable, deterministic verification methods thus forms a major bottleneck in spacecraft autonomy and safety — a gap that rigorous techniques such as Taylor models [1] are uniquely positioned to address.
Project goal
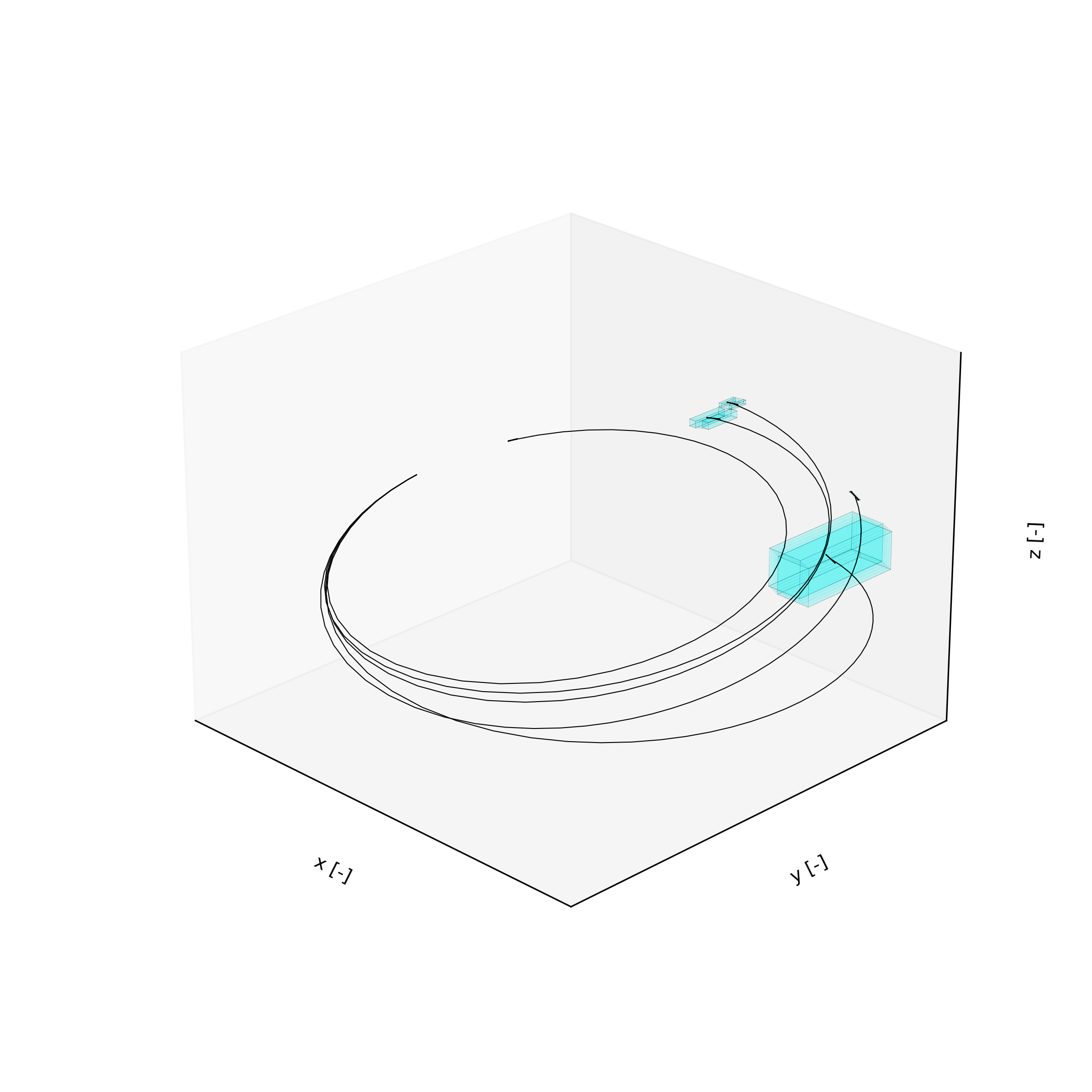
The aim of the project is to develop and implement an accelerated Taylor model algebra, to enable the fast, scalable verified integration of complex dynamical systems. An implementation has been devised that leverages Bernstein polynomials, and in particular the matrix method for Bernstein polynomial bounding [2], which was subsequently implemented in audi. Simplified dynamical systems have been tested, such as a three-dimensional orbit with Keplerian dynamics, visualized in the figure below. In preliminary comparisons with TaylorModels.jl — one of the main open-source alternatives, the audi implementation is slightly slower for univariate polynomials, is 5 to 15 times faster for bivariate polynomials, and 8 to 155 times faster for trivatiate polynomials. Moreover, the remainder bound is identical for uni- and bivariate polynomials, while audi's trivariate remainder bounds are orders of magnitude tighter than the TaylorModels.jl counter part.
References
- Makino, Kyoko. Rigorous analysis of nonlinear motion in particle accelerators. Michigan State University, 1998.
- Titi, Jihad, and Jürgen Garloff. "Matrix methods for the tensorial Bernstein form." Applied Mathematics and Computation 346 (2019): 254-271.